9639. Big array of Dino

Once, when Dino was solving a problem related to arrays, he saw that the size of all arrays is at most 10⁶. Since Dino is a dinosaur, this number seemed very small to him. Therefore, he decided to create a big array.

Dino first creates an empty array and selects n pairs of numbers: (a₁, b₁), (a₂, b₂), ..., (a_n, b_n). Then for each of these pairs he inserts into array the number b_i a_i times. For example, if the first pair is (3, 5), the number 5 will be inserted into array 3 times. After that, Dino decides to arrange this array in non-decreasing order, but since the array is very large, Dino’s computer cannot perform this arrangement. He is interested in the k-th (the array is numbered starting from 1) number. Help Dino to find this number.

Input. First line contains number n (1 ≤ n ≤ 10⁵). Each of the next n lines contains pair (a_i, b_i) (1 ≤ a_i, b_i ≤ 10⁵). The last line contains number k. It is guaranteed that k-th number exists in array.

Output. Print the k-th number in non-decreasing array.

Sample input	Sample output
3 1 2 3 6 2 1 3	2

SOLUTION

data structure map

Algorithm analysis

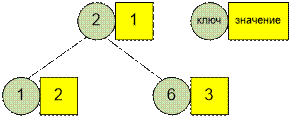
Declare the map data structure. For each pair (a_i, b_i) add a_i to m[b_i]. The map keys will be the numbers of array, the associated values will be the number of times the keys occur in array.

Sum up the number of elements in array by iterating over the map starting from the smallest key and adding up the associated values. As soon as the sum reaches the value of k, the key (the k-th element of array) will be found.

Example

The map data structure after adding three pairs from sample will look like this:

The array in the sample contains two 1, one 2, and three 6. The third number after sorting is 2.

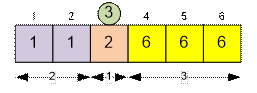
Consider the process of finding the third element (k = 3) in the array.

1 Iteration. k = 3, m[1] = 2. Check: m[1] ≥ 3? No, subtract m[1] from k, k = 3 – 2 = 1.

2 Iteration. k = 1, m[2] = 1. Check: m[2] ≥ 1? Yes, the required element of the array is the key of the current vertex of the map, that is, the number 2.

Algorithm realization

Declare the map data structure.

map<int, long long> m;

Read the input data. For each pair (a_i, b_i) add a_i to m[b_i].

scanf("%d", &n);

for (i = 0; i < n; i++)

{

scanf("%d %d", &a, &b);

m[b] += a;

}

Iterate over the map structure in ascending order of keys. Subtract associated values from k. As soon as the associated value for the next key is at least k, then the corresponding key is the k-th element of array.

scanf("%lld", &k);

for (iter = m.begin(); iter != m.end(); iter++)

{

if ((*iter).second >= k) break;

k -= (*iter).second;

}

Print the answer.

printf("%d\n", (*iter).first);